Una (ulteriore) semplice dimostrazione del Teorema di Morley

Il “Teorema di Morley” afferma: In un triangolo si trisechino gli angoli interni. I tre punti di intersezione delle trisecanti adiacenti formano un triangolo equilatero.

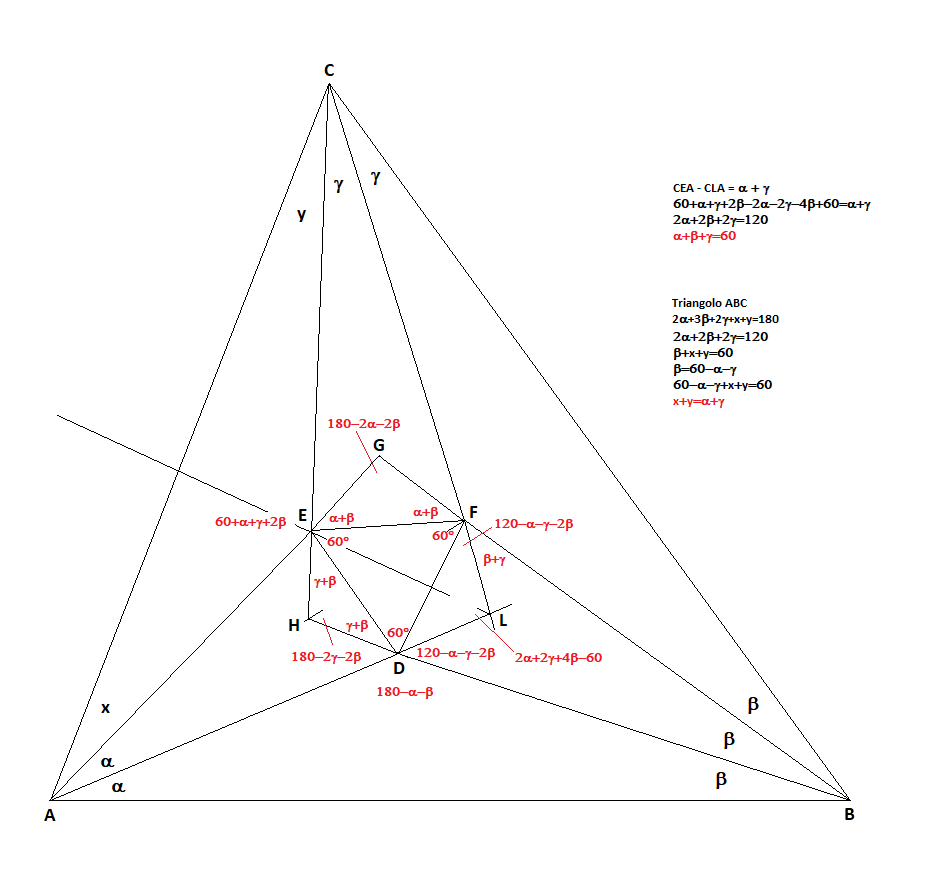
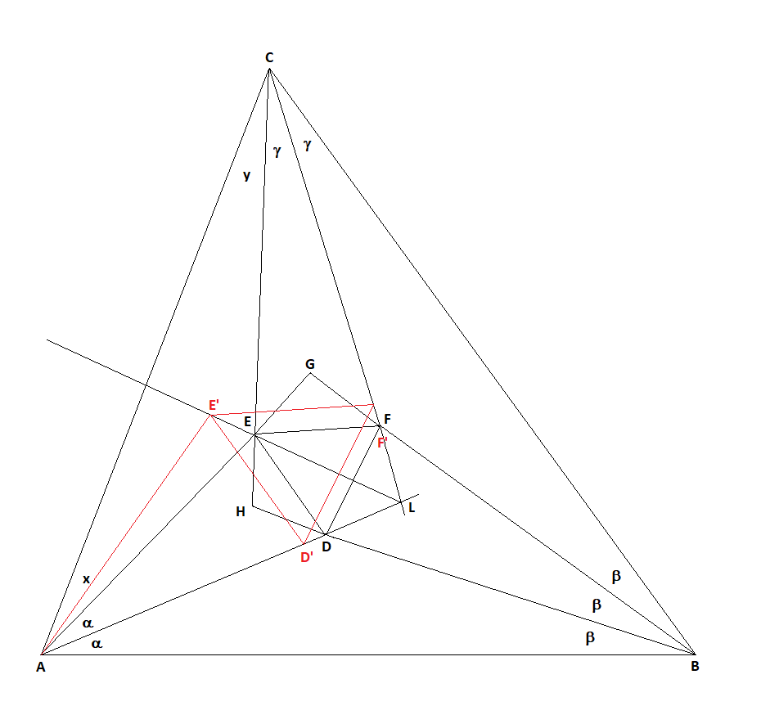
Sia dato un triangolo qualsiasi ABC in cui le misure dei tre angoli A, B e C siano indicate rispettivamente come 3α, 3β, 3γ.

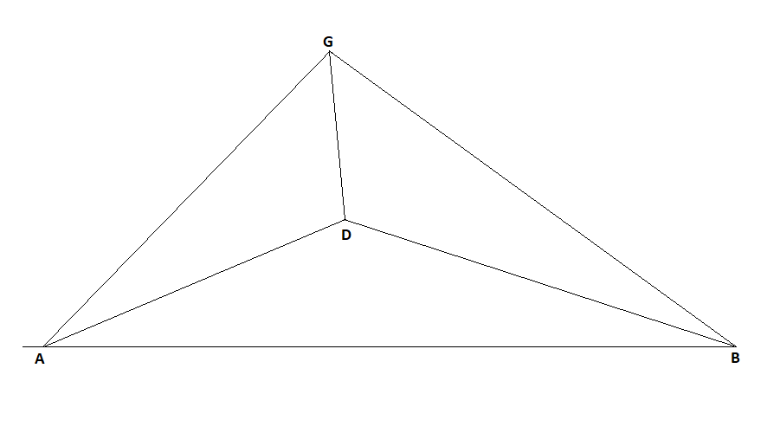
Si costruisca il triangolo ABG avente per angoli alla base 2α e 2β mentre l’angolo al vertice G misurerà, ovviamente, 180° - 2(α + β).

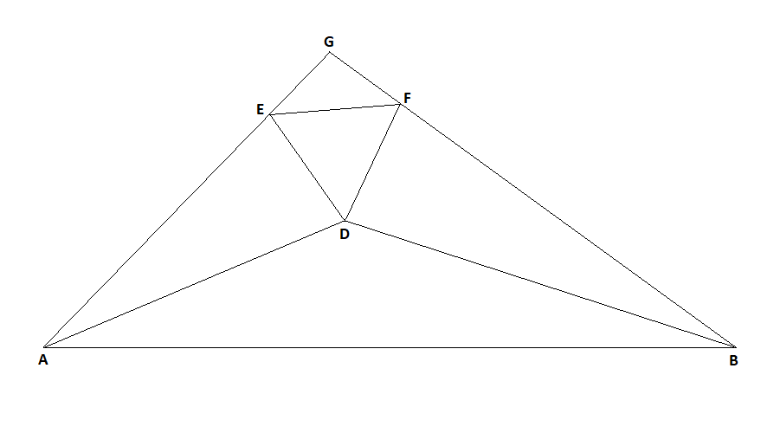
Tracciate le bisettrici del triangolo ABG determiniamo il punto di intersezione D, incentro dello stesso triangolo. Dal punto D è possibile tracciare due segmenti DE e DF tali che gli angoli EDG e GDF abbiano entrambi un’ampiezza di 30°. È facilmente dimostrabile che il risultante RDF è un triangolo equilatero.

Dal punto B si traccia una semiretta che forma un angolo GBY, esterno al triangolo ABG e congruente all’angolo DBF.

Tracciata la normale al lato ED dal punto F, vertice del triangolo equilatero, si determina il punto H, intersezione di questa con il prolungamento di BD, segmento di bisettrice.

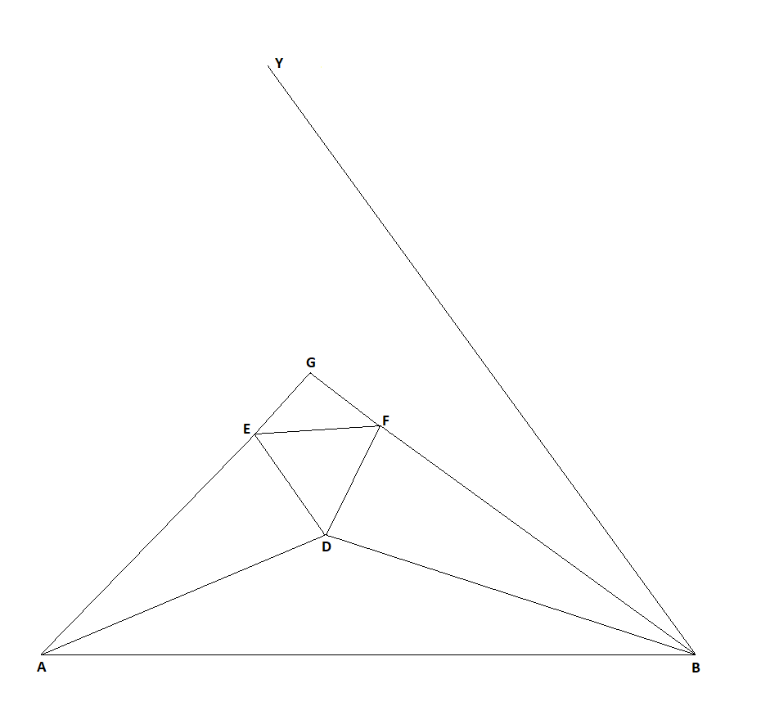
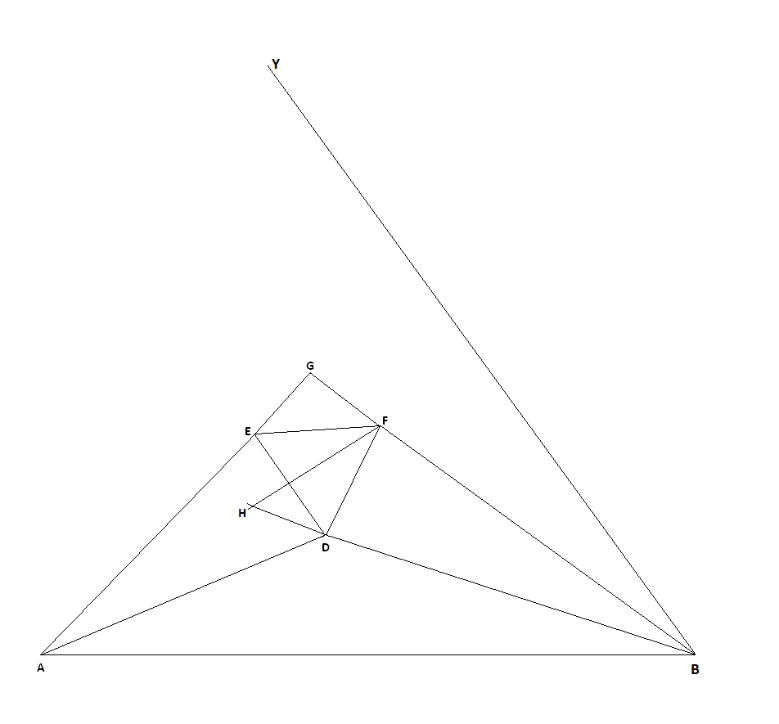
Tracciato il segmento HE e prolungato oltre al punto E, si individua il punto C, intersezione con la precedente semiretta.

HF, per ovvi motivi, giace sulla bisettrice dell'angolo BHC, F è sulla bisettrice dell'angolo DBC, pertanto F è incentro del triangolo CHB e BF è bisettrice dell'angolo HBC.

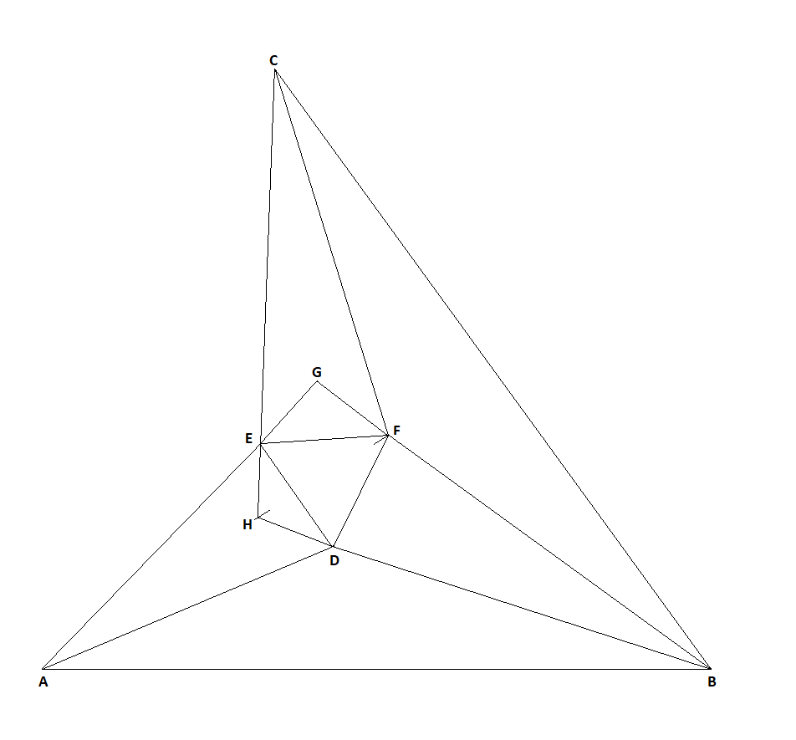
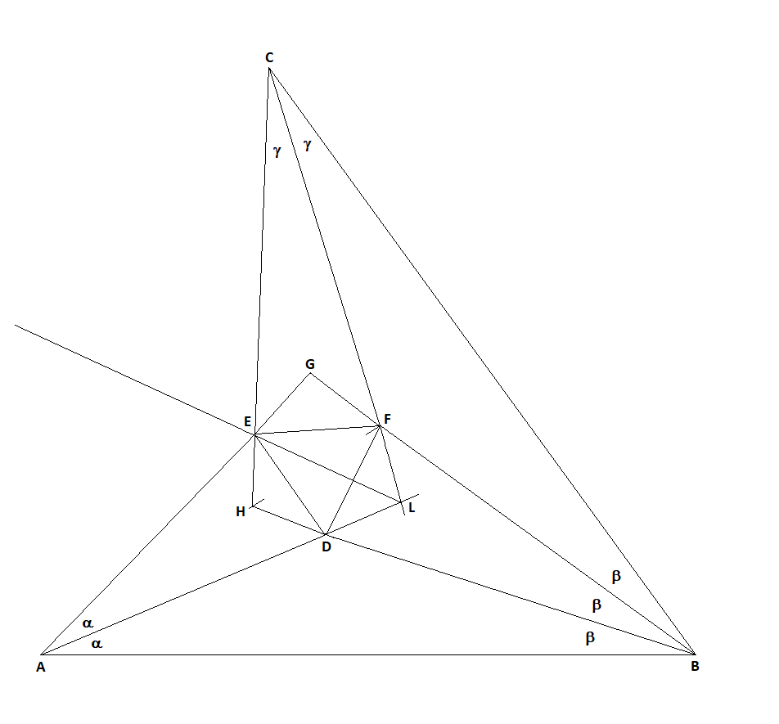
Prolungati il segmento AD ed il segmento BF si intercetta il punto L

Chiamati provvisoriamente γ i due angoli LCH e BCL, resta da dimostrare che CAE è congruente a GAL quindi HCA è congruente a LCH, perciò il punto E incentro del triangolo ALC, dunque derivato dalla trisezione degli angoli in A ed in C. In questo caso l’angolo in A del triangolo ABC risulterebbe somma di tre angoli α e l’angolo in C somma di tre angoli γ, come già denominati due di essi.

Dimostriamo che DL = LF

AGB = 180° - 2(α + β)

EFG = FEG = (180° - AGB)/2 = 90° - AGB/2 = 90° - 90° + (α + β) = α + β

(superfluo segnalare l'ovvietà della natura isoscele del triangolo EFG)

EFD = 60°

BFL = β + γ

LFD = 180° - BFL - 60° - GFE = 140° - (β + γ) - (α + β) = 140° - (α + 2β + γ)

BHC = 180° - 2(β + γ)

(ricordiamo che EDF è triangolo equilatero unico dall’incentro F ai due lati HB e CB)

HDE = DEH = (180° - CHB)/2 = 90° - (90° - β - γ) = β + γ

EDF = 60°

LDB =ADH = α + β

FDL = 180° - HDE – 60° - LDB = 140° - (β + γ) - (α + β)

FLD = 140° - (α + 2β + γ)

LFD = FDL pertanto DL = LF

Il segmento LE giace dunque sulla bisettrice di ALC

Tracciato il segmento AC, lato del triangolo ABC, chiamiamo x e y rispettivamente i due angoli CAE e ECA.

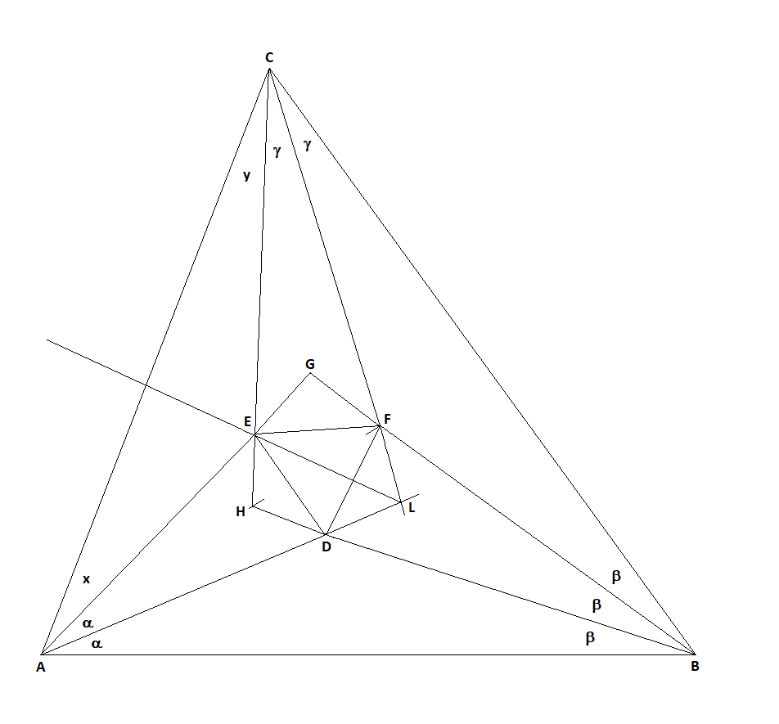
Valgono le relazioni che seguono

Triangolo ABC

(1) x + y = 180° - 2α - 3β – 2γ

Triangolo CHB

CHB = 180° - 2(β + γ)

DEH + HDE = 180° - CHB = 2(β + γ)

DEH = β + γ

Triangolo BGA

BGA = 180° - 2 (α + β)

GEF = EFG = (180° - BGA)/2 = α + β

GEF = α + β

GEH = GEF + DEH + 60°= α + β + β + γ + 60°

GEH = α + 2β + γ + 60°

Triangolo AEC

x + y = 180° – CEA

CEA = GEH

x + y = 180° - α - 2β - γ - 60°

(2) x + y = 140° - α - 2β - γ

Confronto tra la (1) e la (2)

180° - 2α - 3β - 2g = 140° - α - 2β - γ

α + β + γ = 60°

Conclusione

3(α + β + γ) = 180° come dire

3α + 3β + 3γ =180

dalla (1) x + y + 2α + 3β + 2γ = 180°

segue che x + y + 2α + 3β + 2γ = 3α + 3β + 3γ

(3) x + y = α + γ

Questo risultato porta alla certezza che x abbia l’ampiezza di α e y l’ampiezza di γ facendo risultare il punto E come incentro del triangolo ALC.

Infatti, se così non fosse, avremmo un incentro -ancora sulla bisettrice prolungamento di LE- chiamato E’.

Essendo E’A bisettrice dell’angolo LAC, in questo caso avremmo LAE’ = E’AC (angolo x) > α e LCE’ = ACE’ (angolo y) > β perciò x + y > α + γ che è in contraddizione con l’espressione (3).

Perciò, trisecati gli angoli interni di un triangolo, I tre punti di intersezione delle trisecanti adiacenti formano un triangolo equilatero.